НЕКОТОРЫЕ МЕТОДЫ ПРОГНОЗИРОВАНИЯ ВРЕМЕННЫХ ХАРАКТЕРИСТИК РИСКОВ, СВЯЗАННЫХ С КАТАСТРОФИЧЕСКИМИ СОБЫТИЯМИ[*]

 

Виктор Королев, доктор физико-математических наук, профессор, заместитель декана факультета ВМК МГУ им. М. В. Ломоносова

Игорь Соколов, доктор физико-математических наук, член-корреспондент РАН, директор ИПИ РАН

Артем Гордеев, студент МГУ им. М. В. Ломоносова, факультет ВМК

Мария Григорьева, студент МГУ им. М. В. Ломоносова, факультет ВМК

Сергей Попов, студент МГУ им. М. В. Ломоносова, факультет ВМК

Наталья Чебоненко, студент МГУ им. М. В. Ломоносова, факультет ВМК

 

 

В настоящей статье описываются два метода прогнозирования временных характеристик рисков, связанных с катастрофическими событиями в однородных и неоднородных потоках экстремальных событий. Для иллюстрации возможностей этих методов рассмотрена задача прогнозирования риска столкновения Земли с потенциально опасным небесным телом на основе данных Центра по малым планетам Гарвардского университета.

 

Постановка задачи

 

Рассмотрим некоторую систему, подвергающуюся влиянию некоторого фактора, так называемого фактора риска. Предположим, что сила воздействия фактора риска на систему в каждый момент времени характеризуется некоторым числом, причем это число изменяется во времени. Например:

состояние финансовой системы характеризуется финансовым индексом (DAX, NIKKEI, NASDAQ и т. п.);

состояние зданий в сейсмоопасных зонах зависит от силы подземных толчков;

состояние планеты Земля зависит от расстояния, на которое подлетит к ней потенциально опасный астероид.

Будем считать, что абсолютно точно предсказать силу воздействия фактора риска на систему в каждый момент времени в будущем невозможно. Другими словами, будущее развитие фактора риска непредсказуемо, так что значение числа, характеризующего силу воздействия фактора на систему, рассматриваемое как функция времени, образует случайный процесс.

Предположим, что очень большие изменения случайного процесса, характеризующего воздействие фактора риска на систему, неблагоприятно влияют на систему и могут вызвать ее необратимые изменения. Например:

большие скачки финансового индекса, с одной стороны, свидетельствуют о финансовой катастрофе (дефолте), а с другой стороны, усугубляют ее;

резкое увеличение силы подземных толчков, обусловленное землетрясением, ведет к разрушению зданий;

резкое уменьшение расстояния от Земли до какого-либо астероида сверх критического значения, например в силу столкновения этих небесных тел, может привести к глобальной катастрофе.

Вместе с тем, малые флуктуации случайного процесса, характеризующего воздействие фактора риска на систему, вполне допустимы (в таких случаях говорят о фоновом значении фактора риска).

Поэтому с целью предсказания катастроф разумно рассматривать не все изменения случайного процесса, а лишь такие, величина которых превышает некоторый потенциально опасный порог.

Будем говорить, что моменты превышений изменениями случайного процесса потенциально опасного порога в совокупности с самими значениями этих превышений образуют экстремальный случайный процесс. Другими словами, экстремальным процессом назовем последовательность пар , где  – моменты превышений изменениями случайного процесса потенциально опасного порога, а  – величины соответствующих превышений. (В теории случайных процессов такую последовательность пар принято называть маркированным точечным случайным процессом.) Далее по смыслу задачи все значения превышений будут предполагаться положительными:

Среди всех превышений случайным процессом потенциально опасного порога лишь некоторые очень большие влекут катастрофические последствия. Поэтому наряду с потенциально опасным порогом рассмотрим критический порог, превышение которого экстремальным процессом и будем считать катастрофой.

Для удобства точку отсчета (нуль временной шкалы) поместим в то время, которое будем считать настоящим. Тем самым настоящее характеризуется значением .

Поскольку по условию экстремальный процесс считается непредсказуемым, то нельзя точно предсказать момент наступления очередной катастрофы.

Однако можно вычислить или оценить вероятности наступления катастрофы в течение некоторого интервала времени , где . Если  – момент наступления катастрофы, то событие «катастрофа наступила в течение интервала времени » эквивалентно тому, что .

В качестве исходных данных будем использовать информацию о развитии экстремального процесса на некотором интервале времени , где .

Простейшее (примитивное) решение задачи об отыскании вероятности наступления катастрофы в течение интервала времени  при условии  выглядит следующим образом.

Разобьем интервал времени  на непересекающиеся подынтервалы длины . Пусть внутри интервала  поместилось  подынтервалов длины . Подсчитаем количество подынтервалов, внутри каждого из которых наступила хотя бы одна катастрофа. Пусть таких подынтервалов оказалось ровно . Тогда для вероятности наступления катастрофы в течение интервала времени  справедлива оценка:

 

(1)                           ,

 

основанная на классическом определении вероятности как (предела) частоты.

Недостатки такой оценки очевидны. Например,  просто может оказаться равным нулю, и мы получим тривиально оптимистичную оценку; и , и  могут быть (и, как правило, являются) слишком маленькими для того, чтобы обеспечить приемлемую точность оценки; более того, одной-единственной катастрофы может оказаться достаточно для полного уничтожения системы, так что дальнейший сбор информации просто может оказаться невозможным.

К сожалению, именно оценками типа (1) зачастую пользуются на практике для расчетов, связанных с так называемыми большими рисками в страховании, например, при страховании промышленных рисков, связанных с крупными авариями и экологическими катастрофами.

Ниже приведены два подхода к оценке указанных вероятностей наступления катастроф, основанные на довольно сложных математических моделях, но свободные от указанных недостатков. Основная идея этих подходов заключается в том, что для того, чтобы прогнозировать возможности наступления катастроф, не обязательно иметь статистику самих катастроф.

В дальнейшем вероятность некоторого события   и математическое ожидание (среднее значение) некоторой случайной величины  будут обозначаться соответственно  и .

 

Подход, основанный на представлении экстремального процесса в виде маркированного процесса восстановления

 

Рассмотрим однородный поток экстремальных событий и предположим, что длины промежутков времени между превышениями потенциально опасного порога, а именно случайные величины

 

(2)                          

 

стохастически независимы и имеют одинаковое распределение, то есть подчиняются одним и тем же статистическим закономерностям. В таком случае принято говорить, что последовательность случайных величин  образует процесс восстановления.

Будем считать что  – независимые и одинаково распределенные случайные величины. Это означает, что значения этих случайных величин подчиняются одним и тем же статистическим закономерностям, характеризуемым функцией распределения:

 

 

Предположим, что последовательность  статистически независима от последовательности

Критический порог, превышение которого значением  и есть катастрофа, обозначим  (то есть катастрофическое событие формально записывается в виде неравенства ).

Очевидно, что время  наступления катастрофы (то есть время первого превышения уровня  какой-либо из величин ) можно представить в виде:

 

(3)                           ,

где случайные величины  определены соотношением (2), а  – случайная величина, имеющая геометрическое распределение с параметром :

 

 

При этом в силу независимости последовательностей  и  число  слагаемых в сумме (3) независимо от самих слагаемых .

В рамках рассматриваемого подхода краеугольным камнем является утверждение, согласно которому, если , то

 

.

 

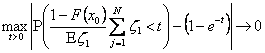Доказательство этого результата можно найти в книге В. В. Калашникова [1].

Из этого утверждения вытекает, что если величина  мала, то справедливо приближенное равенство:

 

(4)                           .

 

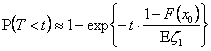Точность аппроксимации формулы (4) характеризует следующий результат, также принадлежащий В. В. Калашникову: пусть , тогда:

 

(5)                           .

 

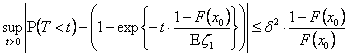Применение соотношений (4) и (5) для прогнозирования временных характеристик рисков, связанных с катастрофическими событиями в однородных потоках экстремальных событий, заключается в следующем: пусть  – произвольное число; решение уравнения

 

 

относительно  обозначим ; смысл значения  – это то время, вероятность наступления катастрофы до которого равна .

Из соображений здравого смысла особый интерес представляют значения , близкие к нулю (соответствующее значение  – это то время, до которого катастрофа скорее всего не наступит), близкие к единице (соответствующее значение  – это то время, до которого катастрофа, скорее всего, наступит), а также .

С учетом соотношений (4) и (5) для  справедливы следующие гарантированные оценки:

 

, где .

 

Особо следует отметить, что при прогнозировании «ожидаемого» времени катастрофы с помощью соотношения (4) можно использовать как математическое ожидание  времени , равное согласно (4):

 

,

 

так и его медиану , определяемую соотношением  и равную в силу соотношения (4):

 

.

 

При этом медиана  почти в 1,5 раза (точнее, в  раз) меньше математического ожидания .

Для того чтобы соотношением (4) можно было пользоваться на практике, необходимо оценить значения параметров  и . Наилучшая оценка для  – это среднее арифметическое значение длин интервалов времени между экстремальными событиями (превышениями потенциально опасного порога) на интервале .

С целью получения оценки величины  требуется построить разумную и адекватную параметрическую математическую модель (приближение) для функции .

Для иллюстрации рассмотрим интересный пример, связанный с определением даты глобальных катаклизмов, которые могут иметь катастрофические последствия. Известно, что к Земле систематически приближаются достаточно крупные космические объекты, столкновение с которыми чревато глобальной катастрофой.

Исследования проводятся на основании данных Центра по малым планетам Гарвардского университета, которые представлены в книге Остина Аткинсона [2]. Это таблица, где содержатся предсказания о датах приближения к Земле на расстояние не более 0,2 астрономических единиц (астрономическая единица, 1 а. е. = 149,6 млн км) комет и малых планет на ближайшие 33 года начиная с июня 1999 года. Всего имеется 191 такое предсказание, для каждого из них известна величина сближения с Землей и месяц предполагаемого сближения.

Расстояние, на которое очередной космический объект приблизится к Земле, представляет собой случайную величину , распределение которой, вообще-то, не известно и подлежит определению (оцениванию). При этом в отличие от рассмотренной ранее формальной модели экстремального процесса интерес представляет не максимальное, а минимальное значение переменной . Ясно, что возможные противоречия легко разрешаются путем рассмотрения случайных величин , вместо .

Формализуем вышесказанное. Существует выборка , , независимых одинаково распределенных случайных величин. Эти величины имеют смысл расстояния между Землей и потенциально опасными астероидами и указаны в таблице.

Предполагается, что даны расстояния от центра Земли до центра астероида. Все подсчеты ведутся в астрономических единицах. Радиус Земли равен  км  а. е.= 0,00004278075 а. е.

В ходе исследования была выдвинута рабочая гипотеза: случайные величины  имеют обратное распределение Парето, определяемое функцией распределения:

 

 

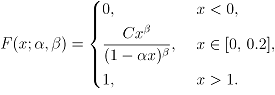
Параметрами этого семейства являются  и . Константа же  определяется из условия .

Легко увидеть, что в таком случае обратные случайные величины , большие значения которых наиболее интересны, имеют распределение Парето с функцией распределения:

 

 

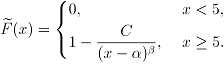
При этом критический порог , превышение которого случайной величиной  означает катастрофу (столкновение астероида с Землей), равен:

 

 

 

Для статистического оценивания параметров  и  использовались несколько методов, но наилучшее согласие получено с помощью метода наибольшего правдоподобия, который дал оценки:

 

 

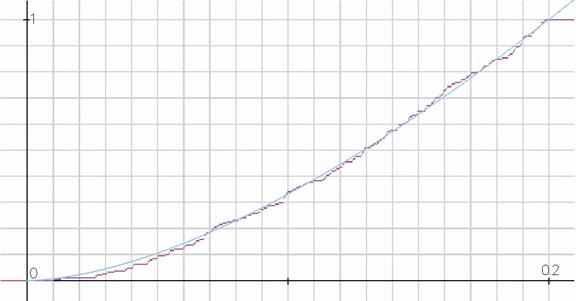
График подогнанной функции распределения Парето с такими параметрами приведен на диаграмме 1, где визуально можно отметить высокое согласие экспериментальных и модельных данных.

Полученные с помощью этих оценок результаты расчетов временных характеристик катастрофы, обусловленной столкновением Земли с астероидом, приведены ниже.

 

 

 

Диаграмма 1

 

Теоретическая и эмпирическая функции распределения (метод максимального правдоподобия)

 

 

 

 

Подход, основанный на представлении экстремального процесса в виде макс-обобщенного процесса Кокса

 

Данный подход ориентирован на ситуацию, более общую, нежели описываемая маркированным процессом восстановления, а именно, согласно этому подходу допустимо различие статистических закономерностей в поведении случайных величин . Во многих случаях разумно считать, что моменты  превышений потенциально опасного уровня случайным процессом, характеризующим значение фактора риска, хаотически рассосредоточены по оси времени, но при этом данный хаос не является однородным в том смысле, что имеются участки оси времени, где точки  размещаются гуще (на таких участках интенсивность превышений высока), чем на других, и наоборот имеются другие участки, где интенсивность превышений мала, то есть точки  размещены реже. Наилучшими математическими моделями неоднородных хаотических потоков событий являются так называемые дважды стохастические пуассоновские процессы, или процессы Кокса (см., например [3]).

Процесс Кокса определяется следующим образом: пусть  – стандартный пуассоновский процесс (однородный пуассоновский процесс с единичной интенсивностью),  – случайный процесс, имеющий почти наверное конечные неограниченно возрастающие непрерывные справа траектории, выходящие из нуля; предположим, что процессы  и  стохастически независимы.

Процессом Кокса называется суперпозиция:

 

 

В таком случае говорят, что процесс Кокса  управляется процессом . В качестве наглядного примера рассмотрим ситуацию, в которой:

 

 

где  – некоторая конечная неотрицательная случайная функция. Можно заметить, что траектории процесса Кокса с таким управляющим процессом совпадают с траекториями неоднородного пуассоновского процесса с (мгновенной) интенсивностью.

Пусть  – точки скачков пpоцесса . Рассмотpим маpкиpованный пpоцесс Кокса, где , где  – независимые одинаково pаспpеделенные случайные величины.

Макс-обобщенным пpоцессом Кокса называется пpоцесс , опpеделяемый для  как:

 

и

 

Общую функцию pаспpеделения случайных величин  как и ранее обозначим , а также используем обозначение:

 

 

При рассматриваемой интерпретации случайных величин  как размера потерь при очередных экстремальных событиях в задаче анализа катастрофических рисков разумно предположить, что, , и .

При анализе редких катастрофических событий особо важную роль играют распределения с тяжелыми хвостами, например распределения типа Парето или сходные с ними по асимптотическим свойствам устойчивые законы. Эти распределения характеризуются тем, что для них выполнено условие о существовании положительного числа  такого, которое для любого :

 

 

Основную роль в рамках второго подхода к прогнозированию катастрофических экстремальных событий играет следующее утверждение (см. работу [4]): символ  обозначает сходимость по распределению.

Рассмотрим теоpему: пусть  – макс-обобщенный процесс Кокса, порожденный последовательностью  и управляемый процессом ; предположим, существуют положительная неограниченно возрастающая функция  и неотрицательная случайная величина  такие, что

 

(10)                         ;

 

предположим также,  и имеется положительное число  такое, что выполнено условие (9), тогда существуют положительная функция  и функция распределения  такие, что:

 

     ;

 

при этом , если  и

 

,

 

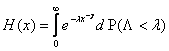если , а функция  может быть определена как:

 

(11)                         .

 

Напpимеp, предположим, что в функции (10) случайная величина  имеет стандартное показательное распределение, тогда  для , а для :

 

.

 

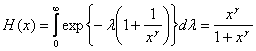Этой функции распределения соответствует плотность:

 

,    .

 

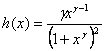Легко увидеть, что у такого распределения  отсутствуют моменты порядка .

Утверждение теоремы позволяет при больших значениях  воспользоваться приближенной формулой:

 

     .

 

Из этого соотношения вытекает, что:

 

(12)                              .

 

Как и ранее, предположим, что  – критический порог: воздействие , превосходящее порог , ведет к катастрофе. Рассмотрим задачу: в течение какого интервала времени практически достоверно можно гарантировать отсутствие катастрофического воздействия?

Решение этой задачи основано на том, что в силу невырожденности предельного распределения  можно сделать заключение о том, что поведение случайного процесса ,  сходно с поведением неслучайной функции , . Самую грубую прикидку вызывающего интерес значения продолжительности интервала времени без катастроф можно получить, решив относительно  уравнение:

 

(13)                         .

 

По крайней мере, если выполнено условие нормировки , «синхронизирующее» единицы измерения времени в процессах     и   , то решение  уравнения (13) правильно передает порядок времени ожидания катастрофы.

Более точную оценку дает следующий подход: пусть  –заданная вероятность практически невозможного события, так что  – вероятность практически достоверного события,  – событие, означающее, что в течение интервала времени  произошло катастрофическое событие; потребуем, чтобы это событие было практически невозможным и для определения значения  воспользуемся соотношением (15), из которого вытекает, что ; обозначив квантиль порядка a функции распределения H через  для определения искомого  получим уравнение ; вспомнив приведенное выше в формулировке теоремы определение функции , получим следующее соотношение, связывающее функцию распределения ущерба , функцию , являющуюся «неслучайным аналогом» случайной накопленной интенсивности  потока экстремальных событий, величину критического порогового значения  и достоверность нашего вывода : .

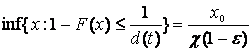Например, пусть функция , гарантирующая стохастическую регулярность накопленной интенсивности потока экстремальных событий, тождественно равна , причем предельная случайная величина  как и в предыдущем примере имеет стандартное показательное распределение, случайные величины  имеют общее распределение Парето с параметром g: , тогда, очевидно, что при достаточно больших   в то время как 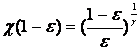, так что .

При этом решение «прикидочного» уравнения (13) в рассматриваемом случае имеет вид .

 

Конкретные временные характеристики глобальной катастрофы, вызванной столкновением с потенциально опасным астероидом. Выводы

 

Оба подхода, описанные выше, были применены к анализу данных из уже упоминавшейся книги Остина Аткинсона [2] с целью получить оценки моментов времени:

, до которого с вероятностью 0,9999 столкновение Земли с астероидом не произойдет;

, до которого с вероятностью 0,9999 столкновение Земли с астероидом заведомо произойдет;

– «ожидаемого» времени столкновения Земли с астероидом (при этом в качестве ожидаемого времени катастрофы использовалось математическое ожидание).

При вычислениях рассматривались величины, обратно пропорциональные исходным, с тем, чтобы операцию минимизации можно было эквивалентно заменить операцией максимизации. Это особенно существенно при реализации второго подхода.

Результаты первого подхода, основанного на представлении экстремального процесса в виде маркированного процесса восстановления, приведены в табл. 1 (в годах).

 

 

 

Таблица 1

1225	12 067 059	111 124 077

 

 

 

При реализации второго подхода, основанного на представлении экстремального процесса в виде макс-обобщенного дважды стохастического пуассоновского процесса, установлено, что с очень большой достоверностью точечный процесс появления потенциально опасных событий является пуассоновским (с постоянной интенсивностью, так что функция L(t) является  линейной).

При этом функция  имеет вид .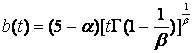

 

Соответствующие вычисления, реализующие второй подход, представлены в табл. 2 (в годах).

 

 

 

Таблица 2

1207	11 976 197	111 141 723

 

 

 

Из табл. 1 и 2 видно, что оба подхода дали практически одинаковые результаты. Это можно объяснить тем, что рассмотренный экстремальный процесс является однородным, поскольку, в частности, на него не влияют субъективные факторы. При этом результаты вычислений позволяют сделать вывод о том, в среднем один раз в 15–25 млн лет Земля претерпевает экстремальные (катастрофические) столкновения со сравнительно большими небесными телами.

Как уже было сказано выше, с очень большой достоверностью точечный процесс появления потенциально опасных событий (потенциально опасных сближений Земли с астероидами) является пуассоновским с постоянной интенсивностью. Пуассоновский процесс характеризуется экспоненциальным распределением времени между последовательными скачками (точками экстремального процесса). От катастрофы до катастрофы реализуется случайное число потенциально опасных событий, причем в случае пуассоновского процесса это случайное число имеет геометрическое распределение, так что интервал времени между катастрофами представляет собой геометрическую случайную сумму независимых показательно распределенных случайных величин. Несложно убедиться в том, что распределение такой геометрической случайной суммы является экспоненциальным. Но, как известно, экспоненциальное распределение обладает свойством отсутствия последействия:  для любых положительных  и . Отсюда вытекает, что, даже если точно знать о том, что после последней на данный момент катастрофы прошло  лет, распределение момента следующего столкновения Земли с астероидом все равно будет таким же, как если этого не знать.

 

 

 

Литература:

 

1. V. Kalashnikov. Geometric Sums: Bounds for Rare Events with Applications. Kluwer Academic Publishers, Dordrecht-Boston-London, 1997.

2. О. Аткинсон. Столкновение с Землей. С.-П.: «Амфора / Эврика». 2001.

3. В. Ю. Королев, В. Е. Бенинг и С. Я. Шоргин. Математические основы теории риска. М.: Физматлит. 2007.

4. В. Ю. Королев и И. А. Соколов. Некоторые вопросы анализа катастрофических рисков, связанных с неоднородными потоками экстремальных событий. – Системы и средства информатики. Специальный выпуск. ИПИ РАН. Москва. 2005, с. 108–124.